Triple Correlation and Laplace distribution
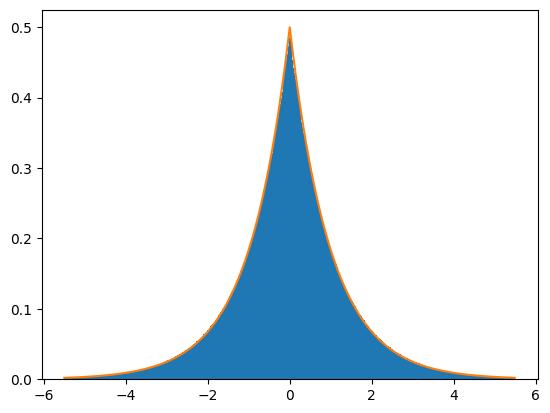
A discrete approximation of the probability density function associated to \(\widehat{\mathcal{S}}_{\pi,\Psi}(X_1,X_2,T,\rho_{\pi})\) where \(L(s,\pi)=\zeta(s), X_1= T^{\frac{1}{2}}\) and \(X_2 = T^{\frac{2}{5}}\) in blue. The probability distribution of a Laplace distribution with mean zero and scaling parameter one in orange.
Triple Correlation and Chi-square distribution
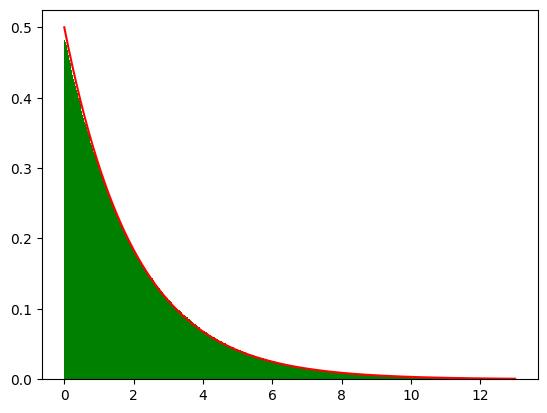
A discrete approximation of the probability density function associated to \(\widehat{\mathcal{S}}_{\pi,\Psi}(X_1,X_2,T,\rho_{\pi})\) where \(L(s,\pi)=\zeta(s), X_1= T^{\frac{1}{2}}\) and \(X_2 = T^{\frac{1}{2}}\) in green. The probability distribution of a Chi-squared distribution with two degrees of freedom in red.
Triple Correlation and Chi-square distribution
A discrete approximation of the probability density function associated to \(\widehat{\mathcal{S}}_{\pi,\Psi}(X_1,X_2,T,\rho_{\pi})\) where \(L(s,\pi)=\zeta(s), X_1= T^{\frac{1}{2}}\) and \(X_2=T^{\alpha_2}\) with \(\alpha_2\) varying between \( (0,1]\) in a discrete equi-spaced manner. This surface contains the previous two graphs as traces at \(\alpha_2 = .4\) and \(.5\), respectively.