Welcome!
This website is the data companion to the paper Surfaces Associated to Zeros of
Automorphic L-functions[1] by Debmayla Basak, Cruz Castillo and
Alexandru Zaharescu. The blue text above is a link to the preprint.
It is recommended to have a copy of the paper on hand while looking through this website.
In this website, you will find a description of our data, visualizations related to the pair and the triple
correlation of the zeros of certain $L$-functions, and tables of moments. Simply click on the corresponding tab
above to see any of this data. To compute our data for $\zeta(s)$, we use the zeros of $\zeta(s)$ found on LMFDB[2] which were
computed by Platt [6]. For the other $L$-functions, we use
Rubinstein's $L$-function calculator lcalc[7].
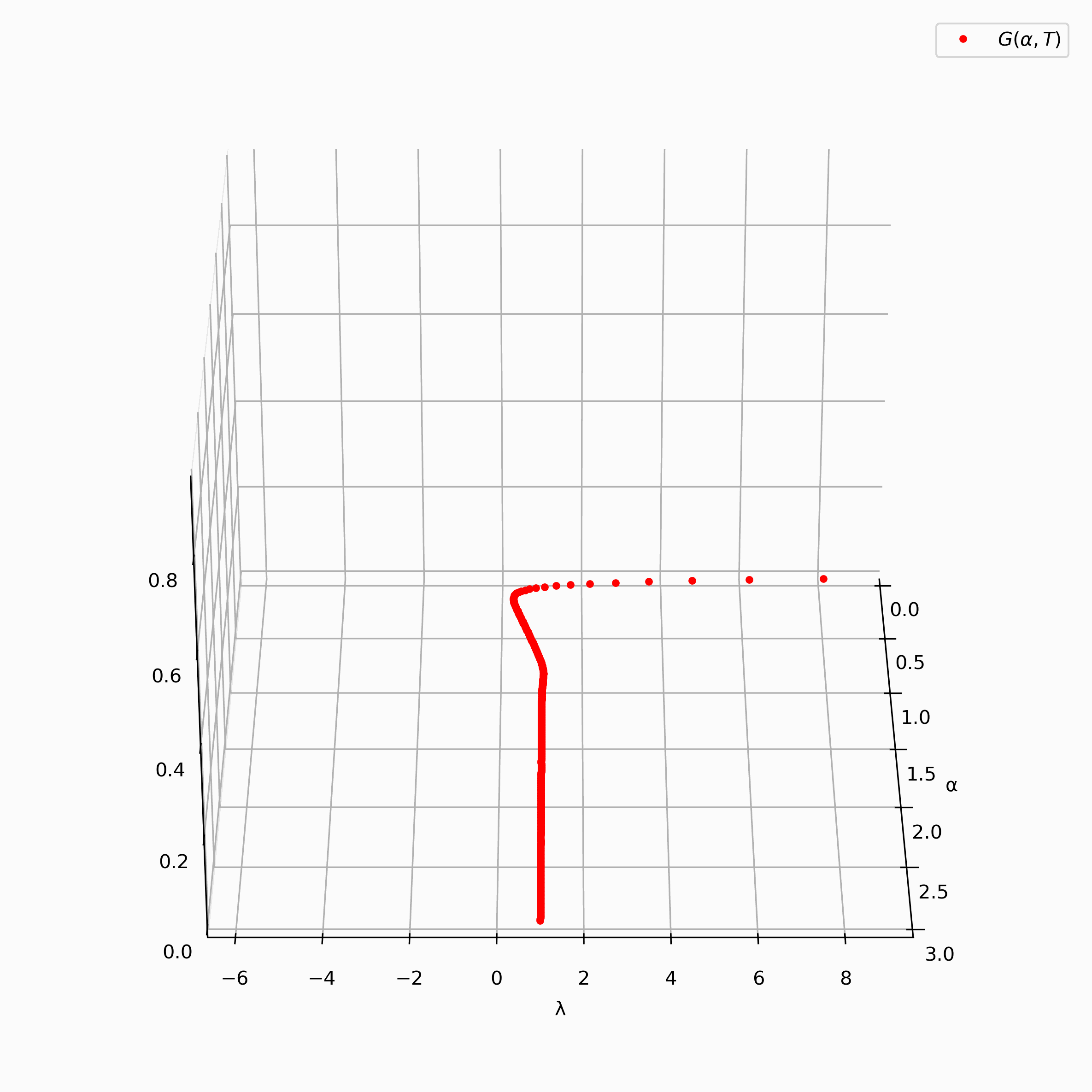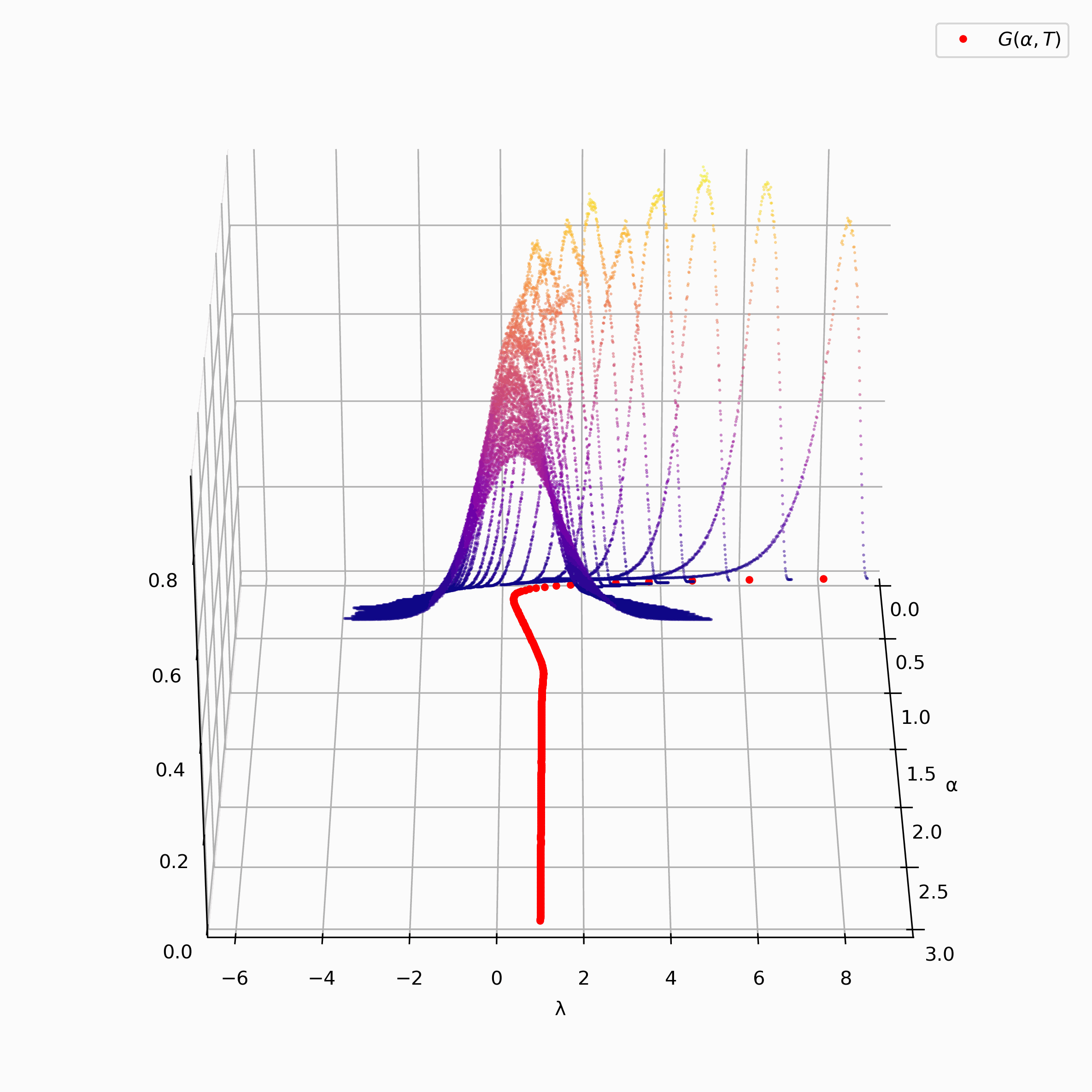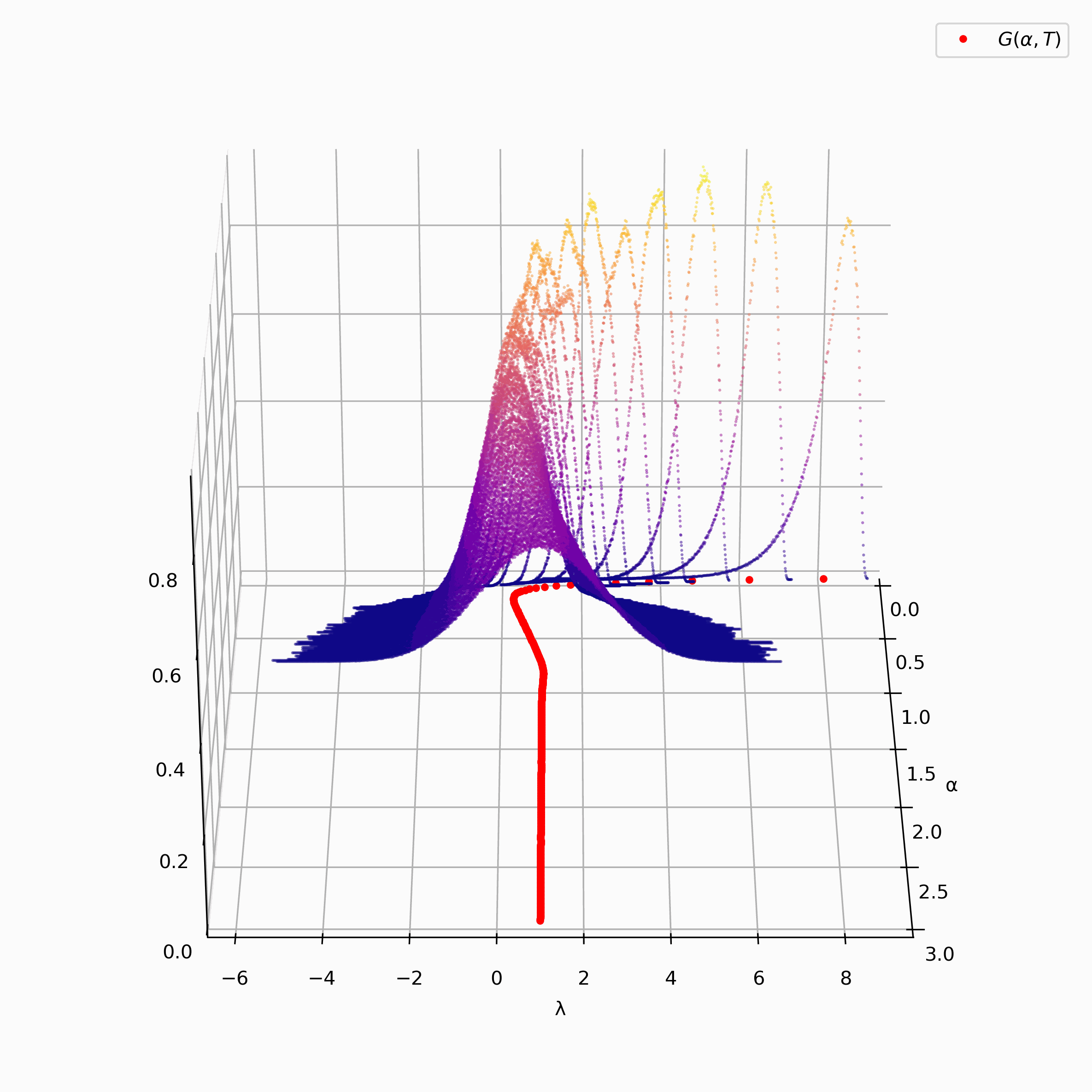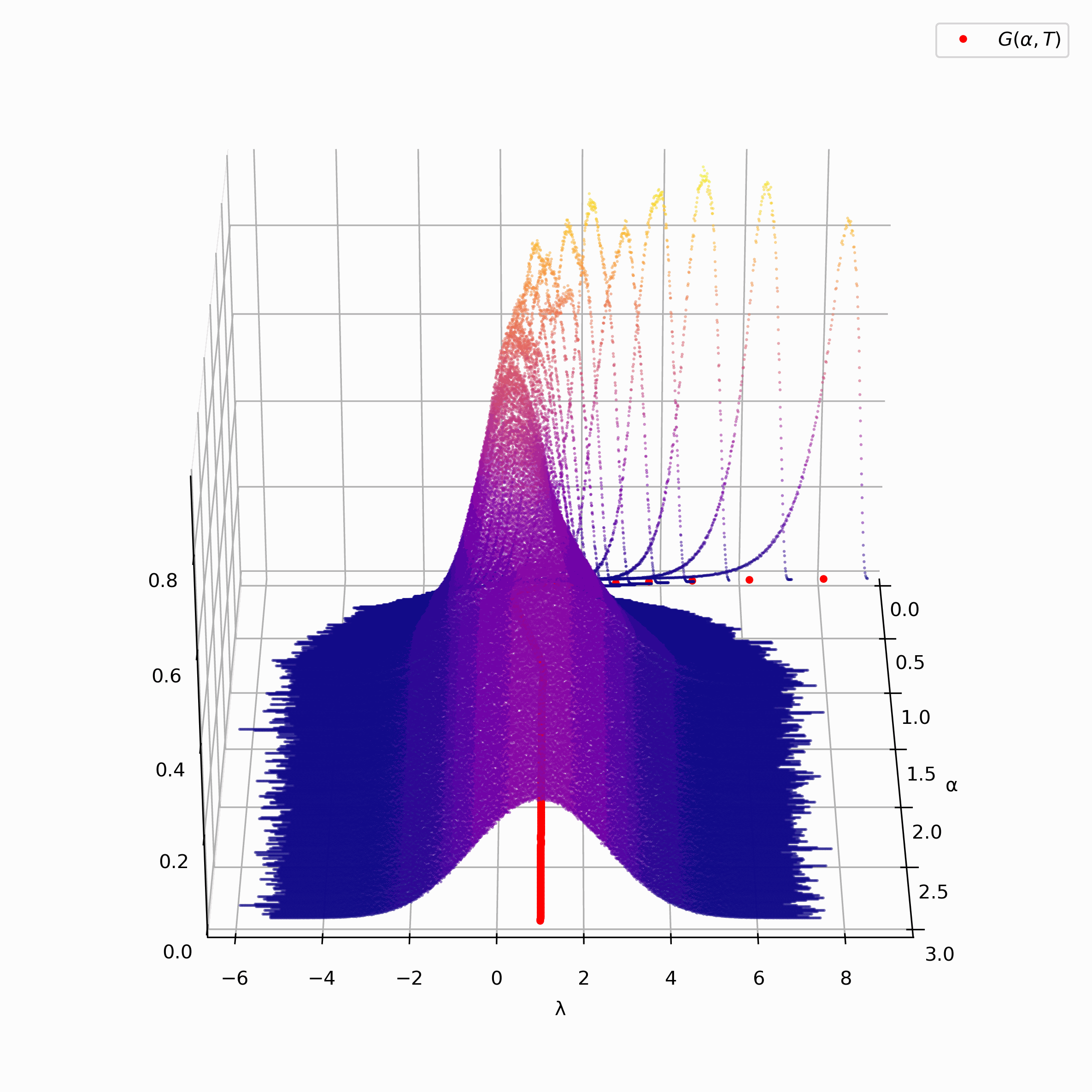
As an example, we include an animation on the right of the unnormalized version of a discrete approximation of the Pair
Correlation Surface generated from the zeros of $\zeta(s).$
In red, we have plotted Montgomery's $F(\alpha)$ function and 500 density histograms generated from the inner sum of Montgomery's $F(\alpha)$ function[4].
As you can see, the surface appears to a bell curve led along Montgomery's $F(\alpha)$ function. For more information on the data, please see the description tab.
We also have data related to the triple correlation of zeros of $\zeta(s).$
Clicking the button to the right under the animation changes the animation to one of the analogous surface for the triple correlation. Here, we have a phase change at $\alpha = .5.$ The $\alpha$
traces morph from a Laplace distribution with mean 0 and scaling factor 1 to a Chi-squared distribution with two degrees of freedom. For more information on the data used to create the animation, please see the description tab.
Finally, the second author would like to acknowledge his support from the National Science Foundation Graduate Research Fellowship Program under the Grant No. DGE 21-46756.